
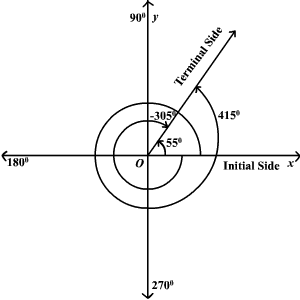
When an angle is negative, we move the other direction to find our terminal side. Now we would notice that it’s in the third quadrant, so we’d subtract 180° from it to find that our reference angle is 4°. For instance, if our angle is 544°, we would subtract 360° from it to get 184° (544° – 360° = 184°). We just keep subtracting 360 from it until it’s below 360. In order to find its reference angle, we first need to find its corresponding angle between 0° and 360°. When an angle is greater than 360°, that means it has rotated all the way around the coordinate plane and kept on going. So, if our given angle is 332°, then its reference angle is 360° – 332° = 28°.
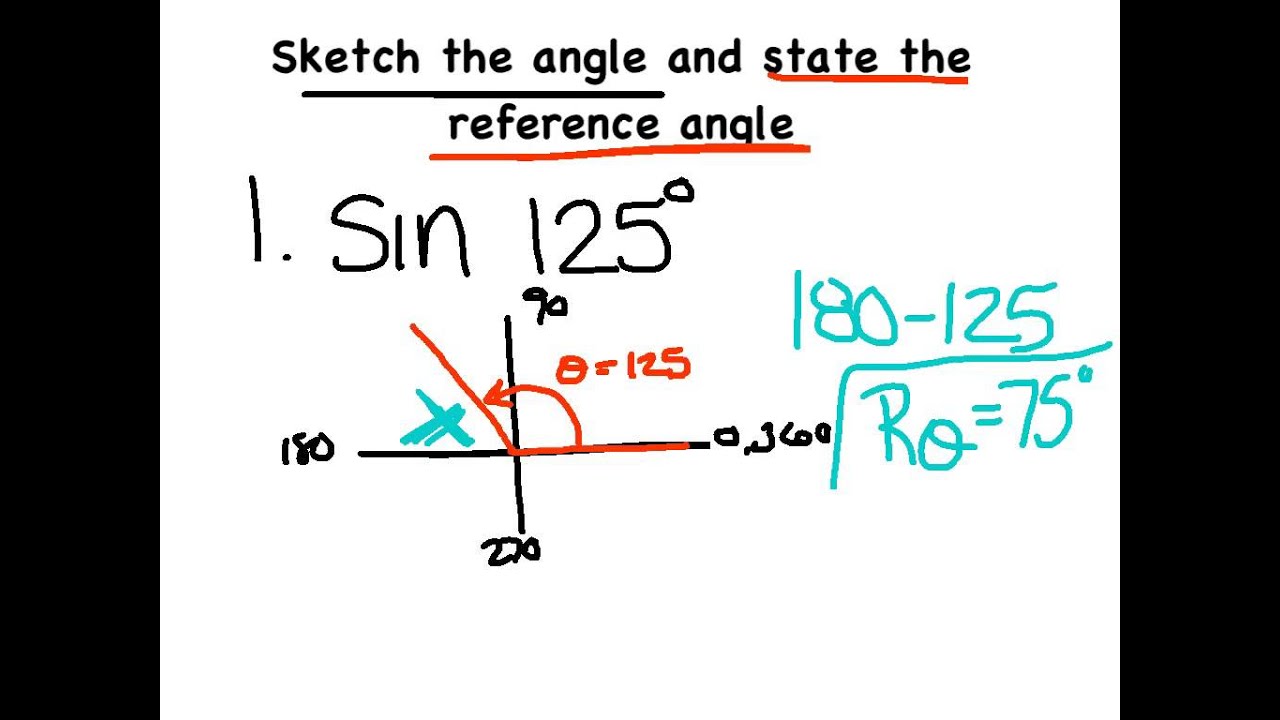
When the terminal side is in the fourth quadrant (angles from 270° to 360°), our reference angle is 360° minus our given angle. So, if our given angle is 214°, then its reference angle is 214° – 180° = 34°. When the terminal side is in the third quadrant (angles from 180° to 270°), our reference angle is our given angle minus 180°. So, if our given angle is 110°, then its reference angle is 180° – 110° = 70°. When the terminal side is in the second quadrant (angles from 90° to 180°), our reference angle is 180° minus our given angle. So, if our given angle is 33°, then its reference angle is also 33°. This makes sense, since all the angles in the first quadrant are less than 90°. When the terminal side is in the first quadrant (angles from 0° to 90°), our reference angle is the same as our given angle. How we find the reference angle depends on the quadrant of the terminal side. How do We Find the Reference Angle without a Calculator? As for the sign, remember that Sine is positive in the 1st and 2nd quadrant and Cosine is positive in the 1st and 4th quadrant. Once we know their sine, cosine, and tangent values, we also know the values for any angle whose reference angle is also 45° or 60°. This is useful for common angles like 45° and 60° that we will encounter over and over again. The sign may not be the same, but the value always will be. The reference angle always has the same trig function values as the original angle. Notice how the second ray is always on the x-axis.
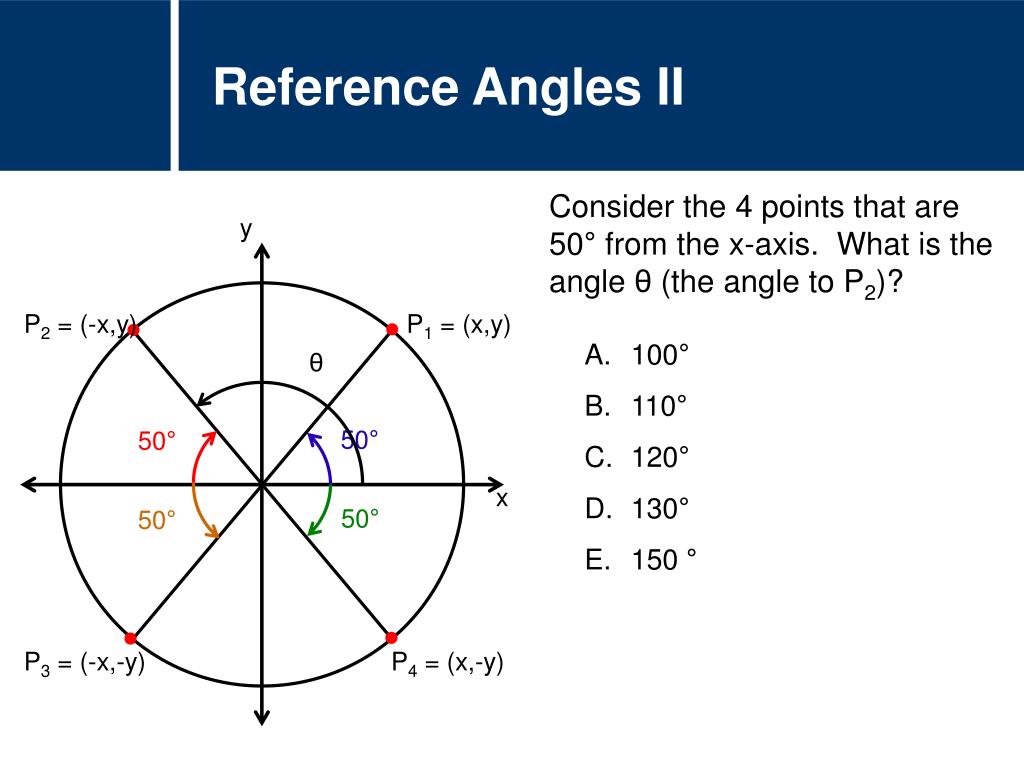
Here’s an animation that shows a reference angle for four different angles, each of which is in a different quadrant. It’s always the smaller of the two angles, will always be less than or equal to 90°, and it will always be positive. This second angle is the reference angle. If we draw it to the left, we’ll have drawn an angle that measures 36°. If we draw it from the origin to the right side, we’ll have drawn an angle that measures 144°. Our second ray needs to be on the x-axis. But we need to draw one more ray to make an angle. Now we have a ray that we call the terminal side. We draw a ray from the origin, which is the center of the plane, to that point. We keep going past the 90° point (the top part of the y-axis) until we get to 144°. We rotate counterclockwise, which starts by moving up. We start on the right side of the x-axis, where three o’clock is on a clock. Let’s say we want to draw an angle that’s 144° on our plane. Each time you add or subtract a multiple of 360 degrees to 60 degrees, you will end up with a coterminal angle of 60 degrees.Go back to Calculators page What is a Reference Angle, anyway? Infinitely many other angles are coterminal to 60 degrees. The -300 degree rotation is pictured here. Therefore, 60 degrees and -300 degrees are coterminal angles. A reference angle always uses the x-axis as its frame of reference. The reference angle is always the smallest angle that you can make from the terminal side of an angle (ie where the angle ends) with the x-axis. The reference angle is the positive acute angle that can represent an angle of any measure. There are an infinite number of coterminal angles that can be found.Īdditionally, do Quadrantal angles have reference angles? Quadrantal Angles: Angles 0°, 90°, 180°, 270°, and 360° do not have reference angles because they are quadrantal angles. Finding coterminal angles is as simple as adding or subtracting 360° or 2π to each angle, depending on whether the given angle is in degrees or radians. Thereof, how do you find the Coterminal angle?Ĭoterminal Angles are angles who share the same initial side and terminal sides. The reference angle is the acute angle (the smallest angle) formed by the terminal side of the given angle and the x-axis. If two angles in standard position have the same terminal side, they are called coterminal angles.


 0 kommentar(er)
0 kommentar(er)
